Blog di Megistone

Megistone - Per non perdere l'orientamento

Esercizio 1: Soluzione

Applicando il teorema di Thevenin, calcolare la corrente I3 nella resistenza R3.

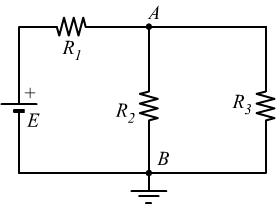
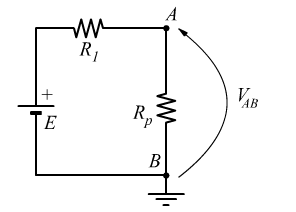
\begin{aligned} E &= 2\;\text{V} \\ R_1 &= 200\;\Omega \\ R_2 &= 4.2\;\text{k}\Omega \\ R_3 &= 800\;\Omega \\ I_3 &=\ ? \end{aligned}

Prevediamo di semplificare col teorema di Thevenin la parte di circuito a monte del taglio indicato in figura.


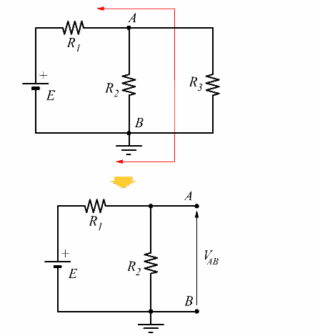
Durante il funzionamento a vuoto (senza il carico R3), la tensione  VAB  coincide con il generatore equivalente  Eeq.
L’unica corrente circolante è quella erogata da  E; la corrente I passa in successione  sulle due  resistenze R1  e R2; le vede dunque in serie:

    \[ I = \frac{E}{R_1 + R_2} = \frac{2}{0,2 + 4,2} = 0,45\;\text{mA} \]

Tale corrente, passando sulla R2,  provoca la caduta di tensione VAB.  Per la legge di Ohm:

V_{AB} = R_2 \cdot I = 4,2 \cdot 0,45 = 1.89\;\text{V}

La resistenza equivalente Req è la resistenza vista ai capi dei nodi A e B con l’unico generatore E  cortocircuitato.

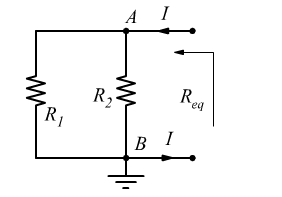
Un’ipotetica corrente che entri dal nodo A ed esca dal nodo B vede tale  sistema di resistenze in parallelo fra loro; per cui:

R_{eq} = \frac{R_1 \cdot R_2}{R_1 + R_2} = \frac{0,2 \cdot 4,2}{4,4} = 0,19\;\text{k}\Omega

Dopo aver calcolato i valori di Eeq e Req ricolleghiamo il bipolo di Thevenin al carico R3.

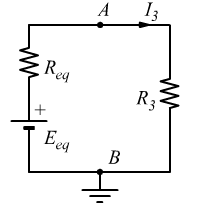
La corrente  I3  che percorre le due resistenze vale:

I_3 = \frac{E_{eq}}{R_{eq} + R_3} = \frac{1,89}{0,19 + 0,8} = \frac{1,89}{0,99} = 1,91\;\text{mA}

Se nel circuito c’è un solo generatore si può fare a meno del teorema.
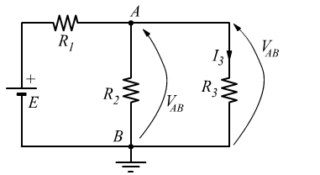
Basta osservare come sia possibile individuare la tensione VAB ai capi dei tre rami (in presenza del carico R3)  facendo il parallelo R2 // R3:

R_p = \frac{R_2 \cdot R_3}{R_2 + R_3} = \frac{4,2 \cdot 0,8}{4,2 + 0,8} = 0,672\;\text{k}\Omega

 

in queste condizioni, per la regola del partitore di tensione si ha:

    \[ V_{AB} = \frac{R_p \cdot E}{R_1 + R_p} = \frac{0,672 \cdot 2}{0,672 + 0,2} = \frac{1,344}{0,872} = 1,54\;\text{V}\]

La tensione VAB  ai cap del parallelo R2 // R3 è uguale alla tensione ai caipi delle due singole resistenze  che costituiscono il parallelo.

così per la legge di Ohm:

    \[ I_3 = \frac{V_{AB}}{R_3} = \frac{1,54}{0,8} = 1,92\;\text{mA} \]

Articoli correlati