Introduzione agli algoritmi
Passiamo ora a descrivere come si possono indicare formalmente ad un computer una serie di compiti da svolgere.
Supponiamo di voler mangiare una pastasciutta e di non aver voglia di cucinarla, basta andare al ristorante e ordinare un piatto di tale portata.
L’algoritmo “mangiare una pastasciutta” è fin troppo esplicito per un operatore umano (al quale già il problema originale sembra probabilmente abbastanza elementare da non richiedere, in apparenza, suddivisioni), ma nel caso di un automa richiederebbe di specificare i passi con ben altra complessità.
Esso si compone dei seguenti passi:
- prendere una pentola sufficientemente capiente (almeno tre litri d’acqua); riempirla per tre quarti d’acqua;
- accendere il fuoco e depositarvi sopra la pentola con coperchio; attendere l’ebollizione dell’acqua;
- aggiungere un cucchiaio raso di sale all’acqua; leggere sulla confezione di pasta il tempo di cottura;
- versare nell’acqua la pasta in ragione di un etto per commensale; attendere la scadenza del tempo di cottura;
- scolare la pasta e condire.
Ciò che abbiamo così scritto dovrebbe in teoria permettere in maniera non ambigua, l’esecuzione del compito di cucinare la pasta. Infatti ogni operazione è perfettamente eseguibile da ogni persona normale e il processo descritto porta in una serie finita di passi all’esecuzione del compito previsto.
Intendiamo con il termine algoritmo una sequenza di istruzioni interpretabili in maniera non ambigua da un dato esecutore, sia esso una macchina od un operatore umano, ognuna di esse eseguibile in maniera operativa e che porta in un numero finito di passi all’assolvimento di un compito.
ESEMPIO
Consideriamo la necessità di dover calcolare la media dei nostri voti in una data materia. Applichiamo la seguente sequenza di passi operativi:
leggi un voto;
aggiorna il totale e tieni conto di quanti voti abbiamo considerato; ci sono ancora dei voti;
se sì ritorna alle operazioni precedenti;
altrimenti calcola la media dividendo il totale per il numero dei voti.
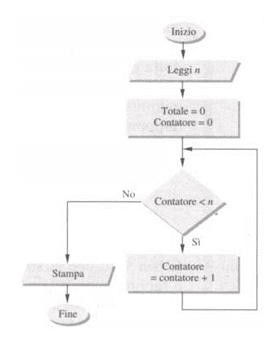
Possiamo schematizzare quanto scritto con il seguente diagramma di flusso
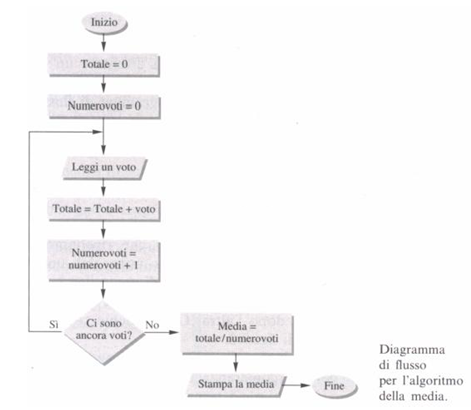
Nel diagramma che abbiamo costruito abbiamo usato dei simboli particolari che adesso definiamo.
Il rettangolo definisce una singola istruzione eseguibile.
Il parallelogramma invece indica un’operazione di immissione dei dati o un’operazione di comunicazione all’esterno dei risultati.
L’ovale indica il punto d’inizio e di fine dell’algoritmo.
Il rombo invece sta ad indicare una proposizione logica che può essere vera o falsa e rappresenta un punto in cui si decide come proseguire nel calcolo all’interno dell’algoritmo.
Connettendo insieme con frecce che indicano la sequenza da seguire, formalizziamo graficamente il concetto di algoritmo.

Connettendo insieme con frecce che indicano la sequenza da seguire, formalizziamo graficamente il concetto di algoritmo.
Prima di proseguire va commentata ancora una particolare istruzione che abbiamo incontrato:
numerovoti=numerovoti+1
Si tratta dell’istruzione di assegnamento. Fa utilizzo del segno uguale in maniera decisamente diversa da come esso viene utilizzato solitamente nell’algebra. Il suo significato, in questo contesto, è indicare che il valore della variabile numerovoti deve aumentare di una unità. Cioè «prendi il valore attuale di numerovoti e sommagli 1» e poi il nuovo valore di numerovoti è il risultato di tale calcolo.
La sequenza
Nello sviluppo di un algoritmo, che, ripetiamo, diventerà poi un programma per computer, sono utilizzabili una serie di elementi costitutivi di base o strutture di controllo. La prima che consideriamo è la sequenza. Si tratta di una serie di istruzioni eseguite in serie una dopo l’altra. Graficamente corrisponde alla rappresentazione di figura.
Come esempio di una sua applicazione consideriamo il calcolo della circonferenza e dell’area del cerchio, conoscendo il raggio. Dapprima determiniamo la soluzione tramite un algoritmo espresso in linguaggio di progetto, poi con l’equivalente diagramma di flusso.
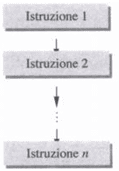
Inizio
Leggi raggio
Area=raggio*raggio*3.14
Stampa Area Circonferenza=2*raggio*3,14
Stampa circonferenza
Fine
Eseguendo una dopo l’altra le operazioni indicate, si raggiunge lo scopo di calcolare i valori desiderati.
Notiamo, ad ulteriore commento dell’algoritmo considerato, che in esso usiamo nomi simbolici per rappresentare i valori dei nostri calcoli ed i valori letti in ingresso oppure stampati in uscita. Tali nomi simbolici sono detti variabili.
Una variabile è dunque un contenitore per valori numerici o di altro tipo all’interno degli algoritmi.
La selezione a due vie
Oltre a mettere in fila una dietro l’altra una serie di istruzioni si possono considerare altri modi per descrivere un compito da eseguire. A volte è necessario prendere delle decisioni prima di proseguire nei calcoli. Si supponga di voler calcolare l’area di un triangolo rettangolo o di un rettangolo nello stesso programma. La sequenza di calcoli da svolgere cambia a seconda dei casi. Nel primo bisognerà leggere i due cateti e poi moltiplicarli tra loro dividendo il risultato ottenuto per due, nel secondo si leggeranno i valori dei due lati del rettangolo moltiplicandoli tra di loro. Vediamo la descrizione di tale programma.
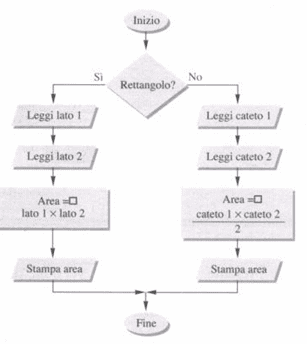
In linguaggio di progetto l’algoritmo viene espresso così:
inizio
se si tratta di un rettangolo allora
leggi lato1 leggi lato2
area=lato1*lato2
stampa area
altrimenti
leggi cateto1 leggi cateto2
area=(cateto1*cateto2)/2
stampa area
fine se
fine
Per descrivere questo algoritmo abbiamo introdotto la prima struttura di controllo fondamentale, presente in qualunque linguaggio di programmazione: la selezione a due vie.
Essa permette di dividere le operazioni da svolgere per portare a termine l’elaborazione dei dati in due sequenze diverse a seconda che una condizione sia verificata o meno.
Possiamo descrivere tale comportamento con il seguente schema:
se <proposizione logica> allora
<sequenza di istruzioni1 >
altrimenti
<sequenza di istruzioni2>
fine se
In grassetto sono evidenziati gli elementi della sintassi (le regole grammaticali del linguaggio di programmazione) che compaiono sempre uguali nella descrizione di tale struttura di controllo.
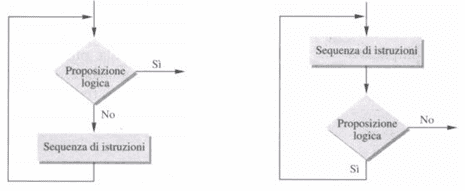
La proposizione logica è un’espressione che fornisce risultato vero o falso. La sequenza di istruzioni1 viene eseguita solo quando la condizione logica è verificata, mentre la sequenza di istruzioni2 viene eseguita quando la proposizione logica è falsa. In modo grafico lo schema corrispondente è in figura:
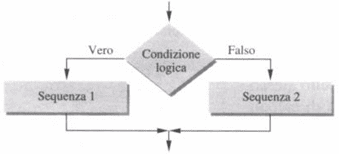
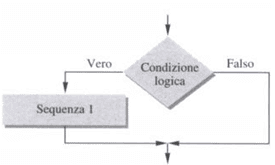
Si tenga presente che esiste una versione in tutti i linguaggi di programmazione della selezione a due vie nella quale la parte relativa alla condizione non verificata, non prevede alcuna esecuzione di istruzioni. In linguaggio di progetto risulta espressa così:
se <proposizione logica> allora
<sequenza di istruzioni) >
fine se
Consideriamo un algoritmo che usa la selezione a due vie:
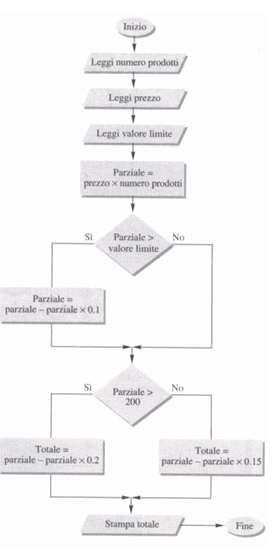
supponiamo di voler calcolare il prezzo totale di una serie di prodotti acquistati da un cliente. Viene calcolato il totale moltiplicando il numero di prodotti per il prezzo del singolo prodotto. Se il prezzo totale supera un certo valore limite viene applicato uno sconto del 10%, altrimenti no. Infine si applica l’IVA che è pari al 20 % fino a € 200 al 15% per importi superiori.
Ecco la soluzione in linguaggio di progetto:
inizio
leggi numeroprodotti
leggi prezzo
leggi valorelimite
parziale=prezzo*numeroprodotti
se parziale>=valorelimite allora
parziale=parziale-parziale*0,1
fine se
se parziale>200 allora
totale=parziale+parziale*0,2
altrimenti
totale=parziale+parziale*0,15
fine se
stampa totale
fine
Le iterazioni Mentre e Ripeti
In alcune situazioni si rende necessario ripetere una serie di operazioni fintantoché non sia soddisfatta una determinata condizione. In tal caso si può utilizzare la seguente struttura:
ripeti
<sequenza di istruzioni>
finché <condizione logica>
che nello stile dei diagrammi di flusso diventa come in figura.
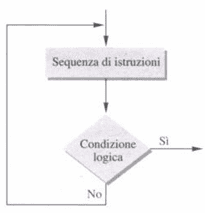
Si tratta di una iterazione con controllo in coda. In pratica si esegue una serie di operazioni, si va a controllare il valore di una data condizione e se questa risulta non ancora verificata, si ripetono le istruzioni già eseguite altrimenti si esce dal ciclo.
ESEMPIO
Supponiamo di avere un elenco di prodotti con i relativi prezzi. Si vuole determinare il prodotto con il prezzo maggiore. Si fa inoltre l’ipotesi di non conoscere a priori il numero di prodotti disponibili per cui ogni volta che l’utente inserisce dei dati al termine dell’operazione il programma chiede se l’elenco è terminato o meno. Ecco una possibile soluzione.
inizio
prezzomassimo=0
ripeti
leggi prodotto
leggi prezzoprodotto
se prezzoprodotto>prezzomassimo allora
prezzomassimo=prezzoprodotto
prodottopiucaro=prodotto
fine se
stampa “vuoi continuare si o no?”
leggi risposta
finché riposta=no
stampa prodottopiucaro
stampa prezzomassimo
fine
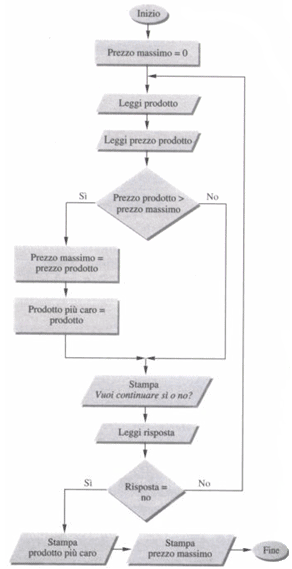
Si tenga presente che con le tre strutture di controllo finora mostrate (sequenza, selezione a due vie, iterazione) è possibile realizzare qualsiasi algoritmo (Teorema di Jacopini Bohm).
Per una questione di flessibilità è possibile utilizzare altre strutture. Un’altra forma possibile di iterazione è la seguente:
mentre <condizione logica> fai
<sequenza di istruzioni>
fine mentre
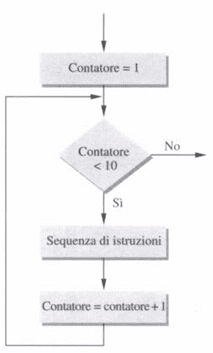
Nella forma di diagramma di flusso questa struttura diventa come in figura.
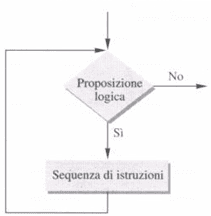
Si tratta di un ciclo di istruzioni che viene ripetuto mentre una condizione risulta essere verificata; quando essa finisce di essere vera si esce dalla struttura.
Si noti che a differenza dell’istruzione ripeti che esegue ripetizioni andando sul ramo No, il mentre ripete seguendo il percorso del Sì. L’altra sostanziale differenza sta nel fatto che entrando nel test, la proposizione logica potrebbe essere fin dall’inizio falsa e dunque la sequenza d’istruzioni potrebbe non essere mai eseguita. Comunque è possibile trasformare un algoritmo che usa una struttura in uno che usa l’altra e viceversa.
Si seguano infatti i diagrammi di figura:
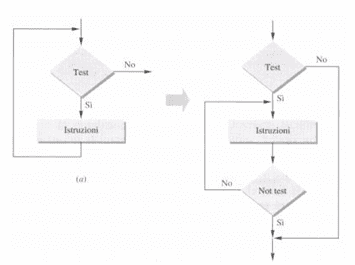
Si noti come effettivamente valga l’equivalenza prima indicata, ma che la realizzazione del mentre con un se ed un ripeti porta ad una struttura meno lineare. Per questa ragione i vari linguaggi di programmazione prevedono il mentre ed il ripeti.
In linguaggio di progetto l’equivalenza vista prima sarebbe espressa così:
mentre <condizione logica> fai
<sequenza di istruzioni>
fine mentre
![]()
se <condizione logica> allora
ripeti
<sequenza di istruzioni>
finché <condizione logica contraria>
fine se
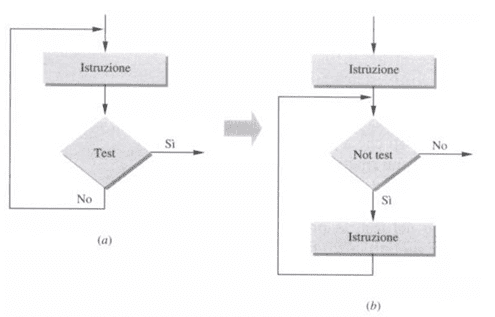
Vediamo l’equivalenza inversa:
ripeti
<sequenza di istruzioni>
finché <condizione logica>
![]()
<sequenza di istruzioni>
mentre <condizione logica inversa> fai
<sequenza di istruzioni>
fine mentre
ESEMPIO
Si supponga di voler calcolare la somma dei primi n numeri, essendo n letto da tastiera. Si comincerà con un totale nullo che viene via via aggiornato fino a quando non si raggiungerà il numero inserito.
Ci vorrà una variabile che, incrementata di un’unità volta per volta, tenga conto di dove si è arrivati.
Ecco la soluzione in linguaggio di progetto.
inizio
leggi n
totale=0
contatore=0
mentre contatore<n fai
contatore=contatore+1
totale=totale+contatore
fine mentre
stampa totale
fine
Alcuni linguaggi di programmazione utilizzano altre forme per gestire le iterazioni; si tratta di due semplici varianti delle strutture di controllo appena considerate.
ripeti finché <condizione>
<sequenza d’istruzioni>
fine sequenza
È una ripeti con la variante che la sequenza di istruzioni viene eseguita almeno una volta, ed il ciclo si esegue quando la condizione logica è falsa.
Essa equivale ad un mentre in cui si inverte la condizione logica. Infatti notate la posizione del sì e del no scambiate tra loro rispetto allo schema di un mentre.
fai
<sequenza di istruzioni>
mentre <condizione logica>
È una mentre con la variante che la sequenza di istruzioni può non essere eseguita, ed il ciclo prosegue quando la condizione logica è vera. Bisogna convincersi che equivale ad un finché in cui si inverte la condizione logica. Infatti notate la posizione del sì e del no scambiate tra loro rispetto allo schema di un finché.
L’iterazione Per
Prendiamo in considerazione un’ulteriore struttura di controllo tipicamente utilizzata nella descrizione di algoritmi. Essa è introdotta per tutte quelle situazioni in cui si vuole eseguire una iterazione sapendo a priori quante volte verrà eseguito il corpo del ciclo. Supponiamo di dover ripetere 10 volte la stessa sequenza di operazioni, ecco come ce la caviamo:
per contatore = 1 fino a 10
<sequenza d’istruzioni>
fine per
È ben vero che la stessa sequenza esecutiva è rappresentabile con le strutture che abbiamo già studiato, ma è una situazione talmente tipica in Informatica che si conviene di utilizzare una specifica istruzione.
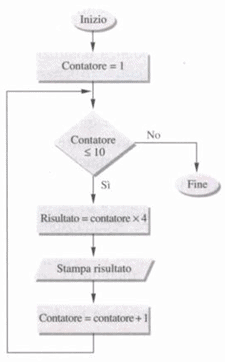
ESEMPIO
Si desidera generare la tabellina del 4.
Banalmente si considerano tutti i numeri dall’1 al 10, si esegue la moltiplicazione per 4 e poi si stampa il risultato.
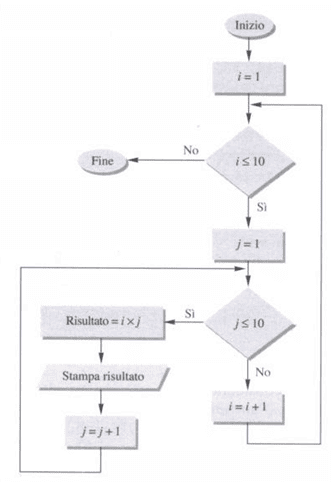
Il diagramma di flusso è illustrato in figura.
Qui di seguito presentiamo la soluzione in linguaggio di progetto:
inizio
per contatore=1 fino a 10
Risultato=contatore*4
Stampa risultato
fine per
fine
Se vogliamo complicarci un po’ la vita generiamo tutta la tavola pitagorica. Dovremo ripetere per 10 volte il procedimento appena visto. Si possono annidare, cioè inserire uno dentro l’altro, due cicli per con due contatori separati, denominati rispettivamente i e j.
Inizio
per i=i fino a 10
per j=1 fino a 10
risultato=i*j
stampa risultato
fine per
fine per
fine
Il confronto tra l’algoritmo espresso in linguaggio di progetto e l’equivalente diagramma di flusso rende conto della maggiore compattezza della notazione scritta rispetto a quella grafica. Per questo, seppur sia importante impratichirsi con notazioni grafiche che spesso vengono utilizzate in ambito informatico, algoritmi di una certa dimensione vengono descritti più spesso in linguaggio di progetto, che, tra l’altro, è molto vicino alla sintassi dei vari linguaggi di programmazione.
Come commento al programma sviluppato, si noti che il per più interno genera tutti i multipli di un dato numero, quello più esterno serve a passare alla prossima «riga» della tavola pitagorica.
La selezione a più vie
Ci rimane da considerare un’ultima struttura di controllo fondamentale: la selezione a più vie. Introduciamola provando a risolvere un esempio pratico con quanto già conosciamo rendendoci così conto della necessità di una notazione più compatta in alcune circostanze.
ESEMPIO
Supponiamo di dover stampare il numero delle ore trascorse in ufficio da un impiegato. Si sa che le ore sono distribuite secondo la tabella.
| Lunedì | 4 |
| Martedì | 8 |
| Mercoledì | 8 |
| Giovedì | 8 |
| Venerdì | 5 |
| Sabato | 7 |
| Domenica | 0 |
Leggendo il giorno della settimana l’algoritmo risponde con il numero corretto. Con ciò che conosciamo affronteremmo il problema nel seguente modo:
inizio
leggi giorno
se giorno=lunedì allora
ore=4
altrimenti
se giorno=venerdì allora
ore=5
altrimenti
se giorno=sabato allora
ore=7
altrimenti
se giorno=domenica
allora
ore=0
altrimenti
ore=8
fine se
fine se
fine se
fine se
stampa ore
Fine
Dovendo considerare 5 diverse ipotesi alternative, si è usata per 4 volte la struttura se … allora … altrimenti. Figuriamoci se avessimo ancor più alternative possibili.
Anche dal diagramma di flusso di figura ci rendiamo conto che può essere utile disporre di una notazione più compatta per casi di scelta multipla.
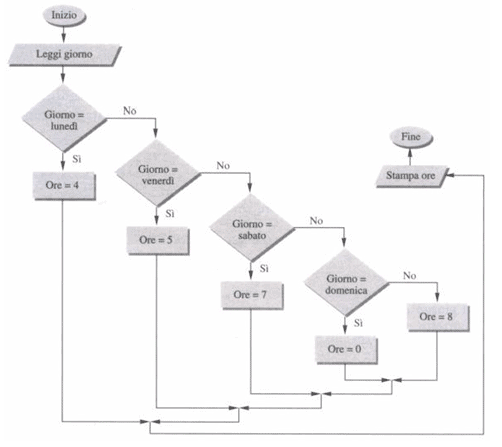
Dunque si introduce la selezione a più vie. Vediamone la struttura sintattica.
seleziona <variabile>
caso <valore 1 >:
<Sequenza di istruzioni1 >
caso <valore 2>:
<Sequenza di istruzioni2>
caso <valore n>:
<Sequenza di istruzionin>
caso altri_valori
<Sequenza di istruzioni_altri_valori >
fine seleziona
Quando si ha a che fare con parecchie alternative determinate da diversi valori costanti della stessa variabile ad ogni possibile caso si associa un gruppo di istruzioni.
È prevista la situazione in cui la variabile di controllo non assuma nessuno dei valori e dunque si aggiunge un caso anche per quest’alternativa.
Quindi, il nostro problema, usando questa struttura, è risolto in modo più compatto con il seguente algoritmo:
inizio
leggi giorno
seleziona giorno
caso lunedì
ore=4
caso venerdì
ore=5
caso sabato
ore=7
caso domenica
ore=0
caso
altri valori
ore=8
fine seleziona
stampa ore
fine
Si noti inoltre la miglior leggibilità della sequenza di istruzioni che compongono l’algoritmo utilizzando questa struttura di controllo. Nel linguaggio dei diagrammi di flusso il seleziona può essere rappresentato con il diagramma di figura.
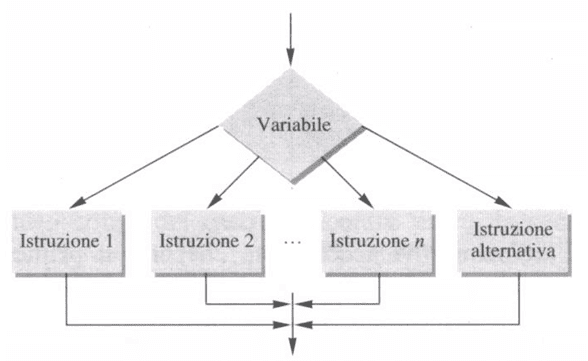
Un’applicazione interessante della selezione a più vie risulta quella della realizzazione della logica di controllo di un automa a stati finiti.
Prendiamo l’ascensore che risultava definito nel suo funzionamento dalla tabella:
| Ingressi | ||||
| Stato attuale | 1 | 2 | 3 | T |
| 1 | 1/F | 2/S | 2/S | T/G |
| 2 | 1/G | 2/F | 3/S | 1/G |
| 3 | 2/G | 2/G | 3/F | 2/G |
| T | 1/S | 1/S | 1/S | T/F |
Possiamo semplicemente trasformare la tabella in algoritmo con una selezione a più vie:
Inizio
Leggi statoattuale
Leggi ingresso
Ripeti
Seleziona statoattuale:
caso 1
seleziona ingresso:
caso 1:
statofuturo=1 uscita=F
caso 2:
statofuturo=2 uscita=s
caso 3:
statofuturo=2 uscita=s
caso t:
statofuturo=t uscita=g
fine seleziona
caso 2
seleziona ingresso:
caso 1:
statofuturo=1 uscita=g
caso 2:
statofuturo=2 uscita=f
caso 3:
statofuturo=3 uscita=s
caso t:
statofuturo=1 uscita=g
fine seleziona
caso 3
seleziona ingresso:
caso 1:
statofuturo=2 uscita=g
caso 2:
statofuturo=2 uscita=g
caso 3:
statofuturo=3 uscita=f
caso t: statofuturo=2 uscita=g
fine seleziona caso t
seleziona ingresso:
caso 1:
statofuturo=1 uscita=s
caso 2:
statofuturo=1 uscita=s
caso 3:
statofuturo=1 uscita=s
caso t:
statofuturo=t uscita=f
fine seleziona
statoattuale=statofuturo
finché uscita=f
fine
{/gspeech}
Esercizi
- Si desidera leggere una sequenza di voti che è terminata da un valore negativo. L’algoritmo deve stampare la media dei voti, il voto migliore ed il voto peggiore. Abbiamo già visto che il calcolo della media consiste in un aggiornamento di volta in volta del totale dei dati inseriti per poter fare alla fine la divisione che ci dà il valore desiderato. Per determinare il valore più grande o più piccolo della serie di numeri invece dobbiamo ragionare in questo modo. Usiamo due variabili, max e min, che all’inizio del procedimento coincidono con il primo valore letto. Ogni volta che acquisiamo un nuovo dato esso va confrontato con max e min, se risultasse più piccolo di min diventerà il nuovo valore più piccolo; qualora fosse più grande di max, sarà max ad essere aggiornato. Questa serie di operazioni va eseguita fino alla fine della sequenza. Dal testo del problema non sappiamo a priori quanti siano i numeri da elaborare. Dunque non possiamo utilizzare un’iterazione per, ma necessita o un ripeti oppure un mentre entro i quali svolgere i calcoli della somma ed i confronti con max o min. Visto che non si conosce il numero di dati dovremo anche aggiornare una nuova variabile da utilizzare nella divisione finale per determinare l’algoritmo. Ecco dunque la soluzione che si profila dal ragionamento appena fatto.
inizio
leggi n
se n>0 allora
contatore=1
totale=n
max=n
min=n
mentre n>0
leggi n
se n>0 allora
totale=totale+n
contatore=contatore+1
se n<min allora
min=n
fine se
se n>max allora
max=n
fine se
fine se
fine mentre
media=totale/contatore
stampa media
stampa max
stampa min
altrimenti
stampa (“la sequenza è vuota”)
fine
- Data una sequenza di 20 numeri interi vogliamo determinare quali di essi sono numeri primi. Ricordiamo che un numero si dice primo quando è divisibile solo per se stesso e per 1. Per determinare se un intero è primo, bisogna dunque provare a dividerlo per 2, poi per 3, poi per 4 e così via. Introduciamo un’operazione che chiamiamo Mod che determina il resto della divisione tra due numeri. 10 Mod 3 =1 poiché 10 = 3 x 3 + 1. Dunque m ed n sono divisibili se m Mod n = 0. Per ogni numero che leggiamo proviamo la divisibilità con tutti gli interi fino ad n/2.
Questa serie di calcoli può essere fatta con le seguenti istruzioni in linguaggio di progetto:
primo=vero
valore=2
ripeti
se n Mod valore=0 allora
primo=falso
altrimenti
valore=valore+1
finché valore>n/2 oppure primo=falso
Si fa l’ipotesi all’inizio che il numero n sia primo. Si imposta il valore iniziale della serie di divisori a 2. A questo punto inizia un ciclo iterativo ripeti. Infatti, per scoprire se un numero è primo dobbiamo dividerlo per tutti gli interi fino ad n/2, se invece non lo è si deve terminare la serie di calcoli non appena abbiamo trovato un divisore. Quindi non sapendo a priori il numero di volte che l’iterazione va ripetuta non possiamo usare un ciclo per. Entro il ciclo si effettua il test sulla divisibilità tra n e valore. Se tale confronto ha successo si segnala il fatto impostando la variabile primo a falso, se no si incrementa valore per provare alla prossima iterazione con l’intero seguente. Segue la condizione di terminazione del ciclo che consiste in un’espressione logica composta. Infatti dalla sequenza si deve uscire in due casi: se la variabile primo vale falso, poiché abbiamo trovato un divisore oppure se abbiamo provato con tutti i numeri fino ad n/2 e non abbiamo trovato divisori. Sarà in questo caso rimasta a vero la variabile primo e dunque abbiamo concluso che il numero non ammette divisori. L’algoritmo a questo punto si completa con un ciclo per che gestisce la ripetizione del calcolo per 10 numeri (il testo specifica questo dato e quindi possiamo usare il per), una struttura se che va a controllare il valore di primo alla fine dei calcoli precedenti e in base al risultato del confronto entro la selezione a due vie, stampa il messaggio adatto. Segue l’algoritmo completo.
inizio
per i=1 fino a 10
leggi n
primo=vero
valore=2
ripeti
se n Mod valore=0 allora
primo=falso
altrimenti
valore=valore+1
finché valore>n/2 oppure primo=falso
se primo=vero allora
stampa “il numero è primo”
altrimenti
stampa “il numero non è primo”
fine per
fine
- Dato il seguente diagramma di flusso si scriva l’equivalente algoritmo in linguaggio di progetto. Che cosa viene calcolato?
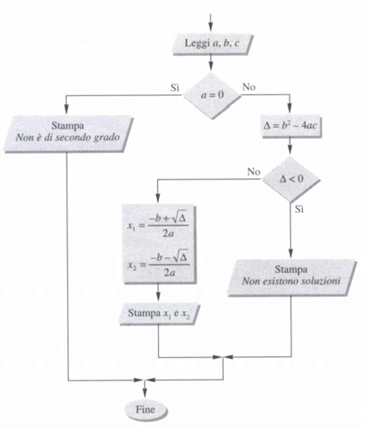
4. Si definisca il concetto di algoritmo.
5. Si indichino le differenze tra un ciclo mentre ed un ciclo ripeti.
6. Si mostri come si può simulare un ciclo mentre con un ciclo ripeti e viceversa.
7. Si simuli con un ciclo mentre ed in seguito con un ciclo ripeti, un ciclo per.
8. Che differenza sussiste tra una selezione ad una via ed una selezione a più vie?
9. Un ciclo ripeti:
a. ha termine quando la condizione logica è vera
b. è un’iterazione a due vie
c. è un ciclo con controllo in testa
d. è una selezione iterativa
10. Il ciclo per:
a. serve per effettuare selezioni
b. non può essere simulato con altri cicli
c. può simulare un ciclo ripeti
d. da un punto di vista teorico può non essere compreso in un linguaggio di programmazione.
11. Il ciclo mentre:
a. ha termine quando la condizione logica è vera
b. è un ciclo con controllo in testa
c. si può simulare con un ciclo for
d. esegue la sequenza di istruzioni al suo interno un numero fisso di volte.
12. La struttura se:
a. è un ciclo
b. è una selezione
c. è un’iterazione
d. è una sequenza.
