Applicazione del teorema di Thevenin
In questo esercizio applichiamo il teorema di Thevenin per calcolare la corrente \(I_3\) nella resistenza \(R_3\). Il circuito è rappresentato come segue:

Parametri del circuito:
\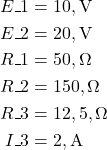
Soluzione
La parte di circuito da semplificare è quella a monte della coppia di nodi \(AB\):

La corrente \(I\) è data da:
\![]()
La tensione ai capi di \(R_1\) è:
\![]()
Il circuito equivalente di Thevenin è quindi:

Dove:
\![]()
Infine, la corrente \(I_3\) è:
\![]()
Questa è la corrente cercata attraverso \(R_3\).
Applicazione del teorema di Thevenin
Applicando il teorema di Thevenin calcolare la corrente \(I_3\) nella resistenza \(R_3\).

\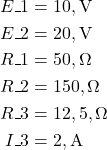
Esercizio 3 soluzione
Anche in questo caso la parte di circuito da semplificare è quella a monte della coppia di nodi \(AB\).

\![]()

L’analisi del ramo su cui si trovano \(E_2\) ed \(R_2\) porta a scrivere la legge di Kirchhoff:
\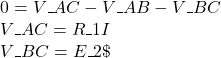
\![]()
Anche in questo caso la \(R_{eq}\) è il parallelo fra \(R_1\) ed \(R_2\).