Esercizio 4 – Calcolo della Tensione VB0V_{B0}
Problema:
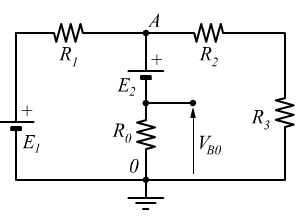
Applicando il Teorema di Thevenin, calcolare la caduta di tensione VB0V_{B0} sulla resistenza R0R_0 nel seguente circuito:
![\[ \begin{aligned} E_1 &= 20 \text{ V} \\ E_2 &= 3,2 \text{ V} \\ R_1 &= 12 \text{k}\Omega \\ R_0 &= 2,88 \text{k}\Omega \\ R_2 &= 18 \text{k}\Omega \\ R_3 &= 20 \text{k}\Omega \\ V_{B0} &= ? \end{aligned} \]](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-b61e5ae8a8a8598a237a3509003f2e36_l3.png "Rendered by QuickLaTeX.com")
[/latex]Dati del circuito:
Fase 1 – Ristrutturazione del Circuito:
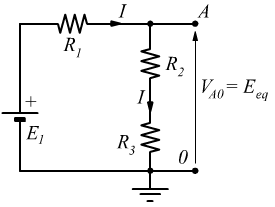
Scambiamo le posizioni del ramo centrale e di quello di destra. Questo è possibile perché entrambi i rami sono collegati alla stessa coppia di nodi AA e 00.
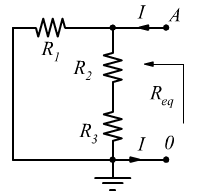
Fase 2 – Semplificazione del Circuito:
Dopo lo scambio, possiamo semplificare il circuito a monte della stessa coppia di nodi:
![<span class="hljs-keyword">\[</span> V<span class="hljs-built_in">_</span>{A0} = E<span class="hljs-built_in">_</span>{eq} <span class="hljs-keyword">\]</span>](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-5d67c8fe857cd6aee78c516397b55f91_l3.png "Rendered by QuickLaTeX.com")
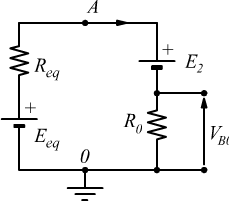
Fase 3 – Calcolo della Tensione a Vuoto:
La tensione a vuoto VABV_{AB} può essere calcolata agevolmente trattandosi di un partitore di tensione:
![<span class="hljs-keyword">\[</span> V<span class="hljs-built_in">_</span>{AB} = <span class="hljs-keyword">\frac</span>{R<span class="hljs-built_in">_</span>2}{R<span class="hljs-built_in">_</span>1 + R<span class="hljs-built_in">_</span>2} <span class="hljs-keyword">\cdot</span> E<span class="hljs-built_in">_</span>1 <span class="hljs-keyword">\]</span>](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-1468af8a1b2a8ce5ec9010b4643048c5_l3.png "Rendered by QuickLaTeX.com")
Fase 4 – Inserimento della Resistenza di Carico:
In un secondo tempo, ai capi di R0R_0 viene posta una resistenza di carico RL=6,6kΩR_L = 6,6 \text{k}\Omega. Si trovi la nuova tensione VB0V_{B0} considerando questa modifica.