Quando si utilizza un computer, si inviano ai suoi circuiti delle informazioni (input). Queste possono essere dati oppure comandi. I dati sono gli elementi sui quali il computer deve operare, i comandi dicono alla macchina cosa deve fare.
Alla fine del lavoro (elaborazione) il computer restituisce altre informazioni che costituiscono l’output.
La parte del computer che effettua l’elaborazione prende il nome di CPU (Central Processing Unit, unità centrale di elaborazione). Per elaborare i dati la CPU si avvale di opportune memorie, dove vengono collocati i dati e i programmi che devono elaborarli. La struttura di un qualunque dispositivo per l’elaborazione delle informazioni è rappresentata da uno schema a blocchi chiamato modello di Von Neumann.
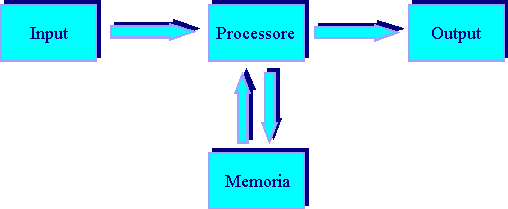
Le informazioni d’ingresso (gli input) possono essere fomite in molti modi. Non necessariamente le fasi di input, elaborazione e output sono rigidamente distinte.
A volte è tutto un susseguirsi di input e output. Per esempio, supponiamo di usare un videogioco che richiede l’impiego del joystick, che è un dispositivo di input, con il quale diciamo al computer come deve far muovere i personaggi, spostare gli oggetti o altro. Il computer elabora continuamente (e velocemente!) tutti questi input e fornisce gli output corrispondenti: movimenti sullo schermo, punteggi ottenuti, cambiamenti di immagini e scenari e così via.
Nei moderni computer troviamo numerosi dispositivi di ingresso e uscita. Immancabili la tastiera e il mouse, ma è frequente trovare uno scanner per l’acquisizione delle immagini, o anche una macchina fotografica digitale. Il joystick è il classico dispositivo di input per i giochi, le tavolette grafiche sono impiegate dai disegnatori.
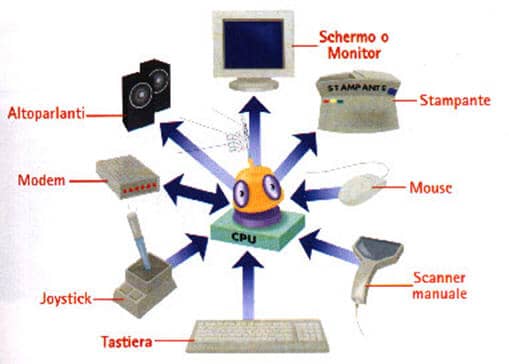
Per i dati in uscita non si può fare a meno di un monitor e di una stampante. I professionisti della grafica ricorreranno ad un plotter in alternativa alla stampante, mentre se le informazioni in uscita sono di tipo sonoro bisogna disporre di una coppia di casse acustiche.
Le informazioni per il PC sono di tipo numerico.
Un computer è in grado di “comprendere” soltanto numeri e, pertanto, tutte le informazioni devono essere trasmesse informato numerico. Come se non bastasse, il nostro incontentabile amico accetta esclusivamente un particolare formato numerico, quello binario. Tutte le informazioni, dalle lettere dell’alfabeto ai suoni, dai colori alle immagini, devono essere espressi in questo formato.
Noi siamo abituati ad usare la numerazione decimale per rappresentare i numeri, il che vuol dire che usiamo le cifre da 0 a 9 per rappresentare le unità. Quando le unità superano le 9, le raggruppiamo in decine. Le decine in centinaia, e via di seguito. Se diciamo, per esempio, che una persona ha 35 anni stiamo usando la numerazione decimale (o in base 10). Il numero 35 significa in effetti 3 decine e 5 unità, come dovremmo già sapere.
I computer usano un sistema diverso in quanto rappresentano tutto mediante due sole cifre, 0 e 1.
Il motivo è semplice: gli esseri umani hanno 10 dita per contare e quindi si sono abituati ad usare una numerazione fino a 10, mentre il computer usa circuiti elettronici che possono avere solo due stati, presenza di segnale elettrico (cioè 1) oppure nessun segnale (e quindi 0).
Facciamo un esempio utilizzando il più semplice e noto dei dispositivi di comando, l’interruttore. Supponiamo che il nostro interruttore comandi una lampada da tavolo. Sappiamo bene che l’interruttore ha due posizioni (che possiamo chiamare stati o livelli logici) e precisamente aperto e chiuso. Se l’interruttore è aperto non passa corrente e la lampada è spenta, viceversa la lampada si accenderà se l’interruttore chiude il circuito. Chiamiamo simbolicamente 0 e 1 questi due stati dell’interruttore. Bene, abbiamo realizzato un circuito binario.

Qualcuno si chiederà: affascinante, ma cosa centra tutto questo con la numerazione, i calcoli, la riproduzione dei suoni e tutto il resto?
Calma, arriviamo subito. L’esempio dell’interruttore serve a fare comprendere in che modo il computer legge e scrive le informazioni nei suoi circuiti e come le conserva in memoria. In un computer sono presenti milioni e milioni di questi “interruttori”, naturalmente microscopici, dove l’unità centrale (per gli amici il microprocessore) colloca i programmi che usiamo e annota diligentemente tutte le nostre attività, dalla scrittura alla grafica. Tutto questo non viene fatto a caso ma secondo regole ben precise.
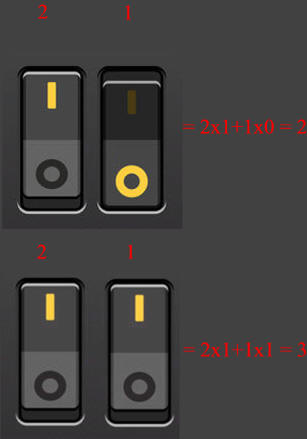
Prendiamo per esempio le nostre cifre decimali. Come fa il computer a memorizzare il numero 5? Chiaramente un interruttore non basta, dato che può ricordare solo uno 0 oppure un 1, cioè un bit di informazione. Evidentemente ne servono molti. Con due interruttori possiamo memorizzare quattro informazioni: 00, 01, 10, 11.
Così è un bel passo avanti, ma non basta. Se usiamo otto interruttori abbiamo a disposizione 256 combinazioni, da 0 a 255. La regola (il codice) per ottenere i numeri decimali è semplice: ciascun interruttore ha un peso diverso, esattamente allo stesso modo in cui le cifre di un numero decimale significano (da destra) unità, decine, centinaia, eccetera. Nel caso dei numeri in codice binario la prima cifra da destra ha peso 1, la seconda 2, la terza 4, e poi 8,16,32, fino a 128 per l’ottavo bit. Se l’interruttore corrispondente è su OFF il peso non viene conteggiato, mentre se è posizionato su ON, sì. Alla fine si sommano i valori ottenuti. Abbiamo usato 8 bit per rappresentare le informazioni, cioè abbiamo usato un byte (1 byte = 8 bit). Il byte è l’unità di misura della memoria nei computer. Un computer di media potenza, oggi, dispone di centinaia di milioni di byte di memoria al silicio (RAM), ossia centinaia di megabyte (MB). Un disco fisso o hard disk per lo stesso computer può contenere decine di miliardi di byte, cioè decine di gigabyte (GB).
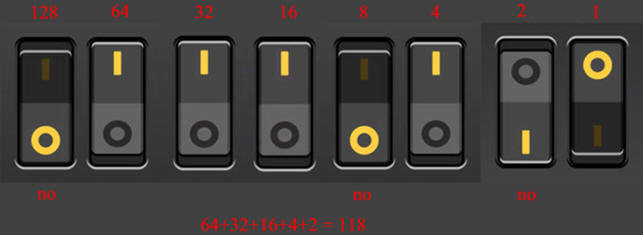
E per i numeri superiori a 255? Facile, si usano più byte.
Così conosciamo il modo in cui un PC rappresenta i numeri. Ma allo stesso modo rappresenta le lettere dell’alfabeto e i simboli della tastiera (punto, virgola, ecc.), i colori da visualizzare sul monitor o da stampare, le note musicali e molte altre cose.
Notiamo infine un particolare importante. Abbiamo detto che con 2 bit possiamo avere quattro combinazioni. Analogamente con tre bit ne abbiamo 8, con quattro arriviamo a 16 e così via. Stabiliamo una regola generale:
se abbiamo a disposizione n bit, il numero di combinazioni possibili è 2n.
Con 8 bit abbiamo, appunto, 28 = 256 combinazioni.
Un binario più breve: l’esadecimale
Il codice binario è normale per un computer ma terribilmente noioso per un essere umano. Al crescere del numero da rappresentare le cifre diventano proprio tante. Per rappresentare in binario l’anno della scoperta dell’America (1492) bisogna scrivere: 10111010100. Qualcuno dirà: ma che problema è? Tanto ci pensa il computer!
| Binario | Decimale | Esadecimale |
| 0000 | 0 | 0 |
| 0001 | 1 | 1 |
| 0010 | 2 | 2 |
| 0011 | 3 | 3 |
| 0100 | 4 | 4 |
| 0101 | 5 | 5 |
| 0110 | 6 | 6 |
| 0111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | 10 |
| 1011 | 11 | 11 |
| 1100 | 12 | 12 |
| 1101 | 13 | 13 |
| 1110 | 14 | 14 |
| 1111 | 15 | 15 |
Corrispondenza fra sistema binario, decimale ed esadecimale.
Vero, ma non dimentichiamoci dei poveri programmatori, quelli che realizzano i programmi con cui scriviamo, disegniamo oppure giochiamo. Si può sintetizzare la scrittura in binario usando la numerazione esadecimale (hex). Questa fa corrispondere ad ogni gruppo di quattro bit un simbolo che lo rappresenta.
Per passare dal binario all’esadecimale bisogna considerare i bit a gruppi di quattro. Dato che come nel nostro esempio sono 11, aggiungiamo uno zero davanti. Otteniamo 010111010100.
Così è tutto più facile. L’anno della scoperta dell’America diventa semplicemente 5D4.
0101 =5
1101 = D
0100 = 4
In realtà il computer vuole numeri esadecimali sempre di due o quattro cifre. Se ne abbiamo solo una oppure tre, basta mettere ancora uno 0 davanti (0hex = 0000 in binario). Quindi scriveremo 05D4 per rappresentare il 1492 nel linguaggio del computer. Per comprendere il motivo di questi aggiustamenti basta ricordare che le lunghezze dei dati accettate dai computer sono fisse: 8 bit, 16 bit, 32 bit, eccetera.
Approfondimento: il codice ASCII
Il codice ASCII è un codice particolare utilizzato per la trasmissione delle informazioni fra elaboratori. In sostanza, ogni cifra numerica, ogni lettera dell’alfabeto (distinguendo fra maiuscole e minuscole) e ogni simbolo presente sulla tastiera (compreso lo spazio, codice 20) è codificato in modo progressivo usando la numerazione esadecimale.
Riutilizzando la regola stabilita poco prima, possiamo calcolare il numero di simboli rappresentabili mediante il codice ASCII. Siccome questo codice usa 7 bit, possiamo rappresentare 27 = 128 simboli diversi. Esiste una versione più aggiornata del codice ASCII, detta ASCII esteso, che usa 8 bit. Con questo codice possiamo rappresentare 256 simboli.
