Esercizio 4

🧮 Esercizi sulle Disposizioni

🔹 Esercizio 4 – Scelta dei rappresentanti

Domanda: In una classe composta da 18 maschi e 12 femmine, si devono scegliere 3 rappresentanti. Quanti sono i modi possibili per sceglierli nei seguenti casi?

Casistica a: Nessuna condizione sui generi
Casistica b: Due maschi e una femmina
Casistica c: Due femmine e un maschio

✅ Soluzione dettagliata:

Si tratta di scegliere 3 rappresentanti tra 30 studenti distinti, quindi useremo le disposizioni semplici (l’ordine è rilevante e non ci sono ripetizioni).

a) Nessuna condizione:
Scegliamo 3 studenti qualsiasi tra i 30 totali:
$D_{30,3} = 30 \cdot 29 \cdot 28 = 24.360$
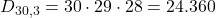
b) Due maschi e una femmina:
Prima scegliamo 2 maschi tra i 18 disponibili, considerando l’ordine:
$D_{18,2} = 18 \cdot 17 = 306$
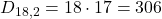
Poi per ciascuna coppia di maschi, possiamo associare una delle 12 femmine:
$12 \cdot 306 = 3.672$
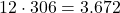
Quindi ci sono 3.672 modi per scegliere due maschi e una femmina.
c) Due femmine e un maschio:
Prima scegliamo 2 femmine tra le 12 disponibili:
$D_{12,2} = 12 \cdot 11 = 132$
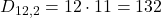
Poi per ciascuna coppia, possiamo associare uno dei 18 maschi:
$18 \cdot 132 = 2.376$
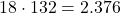
Quindi ci sono 2.376 modi per scegliere due femmine e un maschio.