Esercizio 12: Soluzione

Risoluzione di un circuito elettrico con più maglie – Metodo di Kirchhoff
Nel seguente esercizio analizziamo un circuito composto da più generatori e resistenze. Applicheremo le leggi di Kirchhoff per determinare le correnti nei rami.

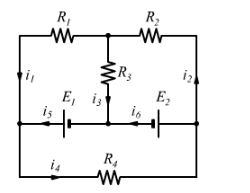
Dati del circuito:
E₁ = 100 V
E₂ = 200 V
R₁ = 20 Ω
R₂ = 30 Ω
R₃ = 10 Ω
R₄ = 20 Ω

Definizione dei nodi e correnti:

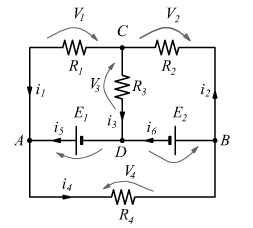
Schema circuito con 4 rami
$\begin{aligned} \text{Nodo A: } & i_1 + i_5 = i_4 \\ \text{Nodo D: } & i_3 + i_6 = i_5 \\ \text{Nodo B: } & i_2 + i_6 = i_4 \end{aligned}$

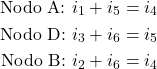
Equazioni delle maglie
$\begin{array}{ll} \makebox[3.3cm][l]{\text{Maglia sup. sinistra:}} & E_1 + V_1 - V_3 = 0 \\ \makebox[3.3cm][l]{\text{Maglia sup. destra:}} & V_2 + V_3 - E_2 = 0 \\ \makebox[3.3cm][l]{\text{Maglia inferiore:}} & V_4 - E_1 + E_2 = 0 \end{array}$

Formule sostitutive con resistenze
$\begin{aligned} & E_1 + R_1 i_1 - R_3 i_3 = 0 \\ & R_2 i_2 + R_3 i_3 - E_2 = 0 \\ & R_4 i_4 - E_1 + E_2 = 0 \end{aligned}$

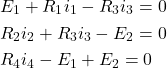
Calcolo diretto per la maglia inferiore
$i_4 = \frac{E_1 - E_2}{R_4} = \frac{100 - 200}{4} = \frac{-100}{4} = -25 \, \text{A}$

Equazioni derivate dai nodi

$\begin{aligned} \text{Dal nodo B: } i_6 = i_4 - i_2 \\ \text{Dal nodo D: } i_6 = i_5 - i_3 \end{aligned}$

per cui $i_4 - i_2 = i_5 -i_3$ da cui $i_5 = i_4 - i_2 + i_3$

PIPPO

Dal nodo A: $i_1 + i_5 = i_4$ sostituendo $i_5 = i_4 - i_2 + i_3$ si ottiene:
$\begin{aligned} & \i_1 + (i_4 - i_2 + i_3) = i_4 \\ & \i_1 + i_3 = i_2 \end{aligned}$

POPO

Equazione maglia superiore sinistra

$E_1 + R_1 i_1 - R_3 i_3 = 0 \Rightarrow i_1 = \frac{R_3 i_3 - E_1}{R_1}$

Equazione maglia inferiore destra

$R_2 i_2 + R_3 i_3 = E_2 \\ \text{Sostituendo } i_1:\\ R_2 (i_1 + i_3) + R_3 i_3 = E_2 \\ R_2 \left( \frac{R_3 i_3 - E_1}{R_1} \right) + R_2 i_3 + R_3 i_3 = E_2$

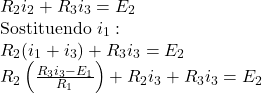
Sostituzione dei valori

$R_2 = 2 \, \Omega, \quad R_1 = 1 \, \Omega, \quad R_3 = 3 \, \Omega, \quad E_1 = 100 \, V, \quad E_2 = 200 \, V \\ 2 \left( \frac{3 i_3 - 100}{1} \right) + 2 i_3 + 3 i_3 = 200 \\ 6 i_3 - 200 + 2 i_3 + 3 i_3 = 200 \\ 11 i_3 = 400 \\ i_3 = \frac{400}{11} \approx 36.36 \, A$
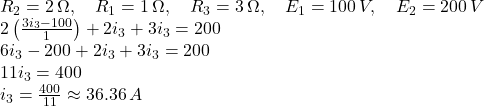
**Titolo: Risoluzione dei nodi in un circuito elettrico**