Esercizio 2: Soluzione

Applicando il teorema di Thevenin calcolare la corrente nella resistenza

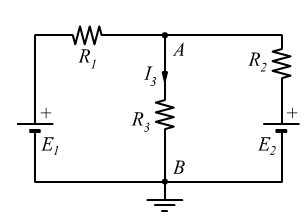
$\begin{aligned} E_1 &= 11\;\text{V} \ E_2 &= 7\;\text{V} \ R_1 &= 2\;\Omega \ R_2 &= R_3 = 1\;\Omega \ I_3 &=\ ? \end{aligned}$

Esercizio 2 – soluzione

Il circuito è stato già analizzato in precedenza con le leggi di Kirchhoff, col teorema di Millman e col principio di sovrapposizione degli effetti.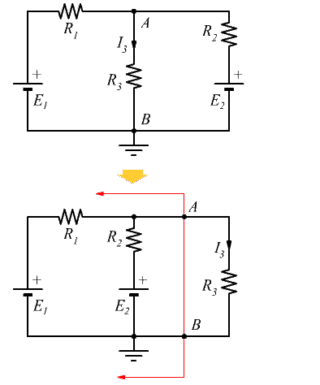

In questo caso possiamo notare come lo spostamento della verso destra nello schema non altera la sostanza dello schema iniziale; in quest’ultimo circuito applichiamo il teorema di Thevenin, semplificando il circuito a monte della coppia di nodi , .

Nel circuito da semplificare, può circolare solo una corrente $I$ che plausibilmente dovrebbe avere il verso indicato in figura, dato che il generatore è maggiore del generatore , e quindi prevale imponendo il verso.

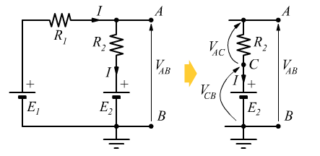
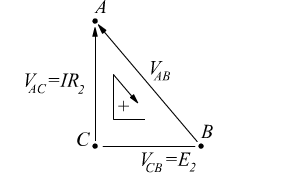
$I = \frac{E_1 - E_2}{R_1 + R_2} = \frac{11 - 7}{2 + 1} = \frac{4}{3}\;\text{A}$

La tensione può essere ottenuta osservando le tensioni sul ramo della . Considerando il nodo intermedio , si riconosce che la può essere ottenuta come composizione della e della .
Infatti, vediamo come sia mentre .

$\begin{aligned} 0 &= V_{AC} + V_{CB} - V_{AB} \ V_{AB} &= R_2 I + E_2 \ V_{AB} &= 1 \cdot \frac{4}{3} + 7 = \frac{4}{3} + \frac{21}{3} = \frac{25}{3}\;\text{V} = E_{eq} \end{aligned}$

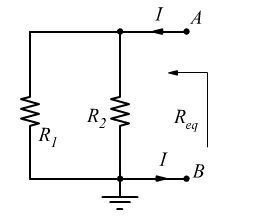
La resistenza equivalente corrisponde alla resistenza vista ai nodi $A$ e $B$ coi generatori cortocircuitati.
In tal caso una corrente entrante in $A$ ed uscente da $B$ ‘vedrebbe’ le due resistenze ed in parallelo fra loro.

$R_{eq} = R_1 // R_2 = \frac{R_1 R_2}{R_1 + R_2} = \frac{2 \cdot 1}{2 + 1} = \frac{2}{3}\;\Omega$

Possiamo ora ricostruire il circuito originario collegando il generatore equivalente e la resistenza equivalente al carico .

$I_3 = \frac{E_{eq}}{R_{eq} + R_3} = \frac{25}{\frac{2}{3} + 1} = \frac{25}{\frac{5}{3}} = \frac{25 \cdot 3}{5} = \frac{75}{5} = 5\;\text{A}$

Articoli correlati

Esercizio 1: Soluzione