Esercizio 5
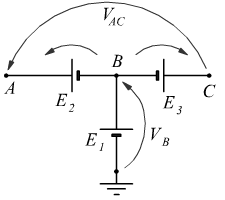
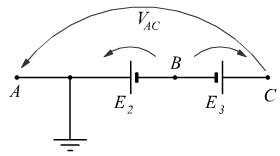
I generatori \(E_1 = 3\,\text{V}\), \(E_2 = 6\,\text{V}\), \(E_3 = 4{,}5\,\text{V}\) sono collegati secondo il seguente schema:
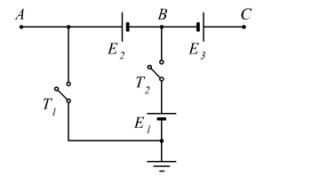
Calcola i potenziali dei punti A, B e C nelle seguenti condizioni:
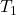- \(T_1\) chiuso e 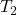\(T_2\) aperto
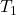- \(T_1\) aperto e 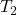\(T_2\) chiuso
Soluzione – Caso 1
Con \(T_1\) chiuso e \(T_2\) aperto, il nodo \(A\) viene collegato alla massa:
\(V_A = 0\,\text{V}\)
Procedendo da sinistra verso destra e applicando la legge delle tensioni, si ottiene:
\(V_{AC} = E_2 - E_3 = 6 - 4{,}5 = 1{,}5\,\text{V}\)
Dunque il potenziale del punto \(C\) è:
\(V_C = V_A - V_{AC} = 0 - 1{,}5 = -1{,}5\,\text{V}\)
Infine, poiché \(E_2\) si trova tra \(A\) e \(B\) con polarità diretta, il potenziale di \(B\) sarà:
\(V_B = V_A - E_2 = 0 - 6 = -6\,\text{V}\)
Soluzione – Caso 2
Con \(T_1\) aperto e \(T_2\) chiuso, il nodo \(B\) si collega al generatore \(E_1\), quindi assume il potenziale:
\(V_B = E_1 = 3\,\text{V}\)
Possiamo calcolare la differenza di potenziale tra \(A\) e \(C\) come:
\(V_{AC} = V_{AB} - V_{CB} = E_2 - E_3 = 6 - 4{,}5 = 1{,}5\,\text{V}\)
Ora, per calcolare \(V_A\) e \(V_C\), procediamo a ritroso rispetto a \(V_B\):
\(V_A = V_B + V_{AB} = E_1 + E_2 = 3 + 6 = 9\,\text{V}\)
\(V_C = V_B + V_{CB} = E_1 + E_3 = 3 + 4{,}5 = 7{,}5\,\text{V}\)
Riassunto finale – Caso 2
- \(V_A = 9\,\text{V}\)
- \(V_B = 3\,\text{V}\)
- \(V_C = 7{,}5\,\text{V}\)