Esercizio 9

Nel circuito di figura è illustrato un collegamento fra generatori:  E₁ = 3 V, E₂ = E₃ = 4,5 V,  E4 = 9 V , E5 = 6 V. Si vuole calcolare la tensione V_AB tra i nodi A e B. Supponendo poi di porre a massa il nodo C, si calcoli i potenziali dei nodi, A e B e si verifichi che V_AB sia rimasta invariata.

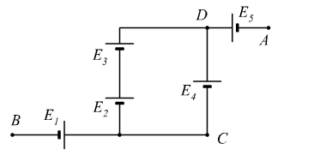
Soluzione – Caso 1

Se il nodo C non è a massa la situazione è come schematizzata in figura. Il parallelo fra i generatori E₂–E₃ ed E₄ è riconducibile ad un’unica f.e.m. fra i poli D e C di valore 9V.

 

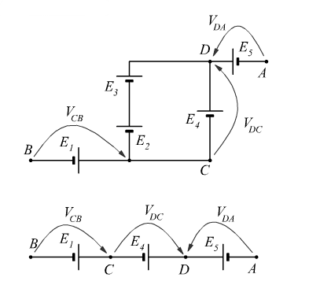
Come si vede V_CB e V_DC concorrono a formare la V_AB, mentre V_DA si oppone.

\( V_{AB} = V_{CB}+V_{DC}-V_{DA} \) \( V_{AB} = E_{1}+E_{4}-E_{5} = 3+9-6 = 6\,\text{V} \)

Non avendo nessun riferimento a massa il bipolo AB è flottante; non è dunque possibile predire il valore che i suoi terminali assumeranno rispetto agli 0 V.

Soluzione – Caso 2

Continua ad esserci il parallelo fra i generatori E₂–E₃ ed E₄ è riconducibile ad un’unica f.e.m. fra i poli D e C di valore 9V.

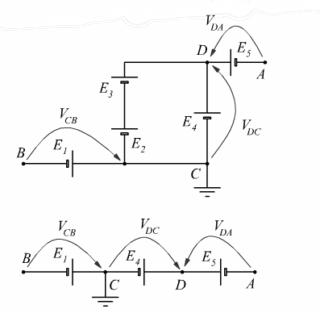
\( \text{Ora C è la massa: } V_C = 0 \)

\( V_{CB} = V_C - V_B = E_1 \Rightarrow 0 - V_B = 3 \Rightarrow V_B = -3\,\text{V} \)
\( V_{DC} = V_D - V_C = E_4 \Rightarrow V_D - 0 = 9 \Rightarrow V_D = 9\,\text{V} \)
\( V_{DA} = V_D - V_A = E_5 \Rightarrow 9 - V_A = 6 \Rightarrow V_A = 3\,\text{V} \)

\( \text{Essendo } V_{AB} = V_A - V_B = 3 - (-3) = 3 + 3 = 6\,\text{V} \) \( \text{Per i potenziali ai nodi A e B non è cambiato niente.} \)