Risoluzione di un circuito elettrico con le leggi di Kirchhoff
In questo articolo vedremo come risolvere un circuito elettrico complesso utilizzando le leggi di Kirchhoff. Il circuito presenta tre resistenze, tre generatori e correnti incognite nei rami. Il nostro obiettivo è determinare le correnti e il valore di una resistenza incognita.
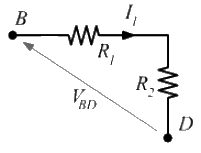
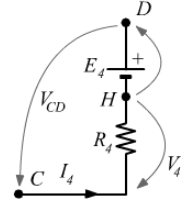
Schema del circuito
Dati del problema
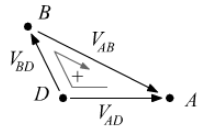
![]() vuol dire che la segnatura della d.d.p. sul tratto BD prevede la freccia su B. Questo concorda con la caduta di tensione provocata dal passaggio della
vuol dire che la segnatura della d.d.p. sul tratto BD prevede la freccia su B. Questo concorda con la caduta di tensione provocata dal passaggio della ![]() su
su ![]() e su
e su ![]() , per la legge di Ohm:
, per la legge di Ohm:
![]()
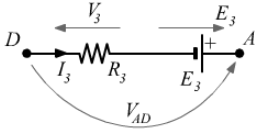
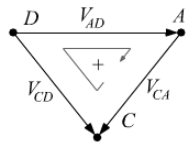
Scrivendo la legge di Kirchhoff per il tratto AD avremo:
![]()
Proseguimento – Analisi completa della maglia
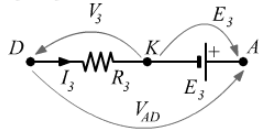
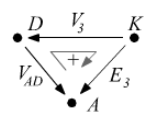
Allo stesso risultato si arriva se sul tratto AD consideriamo il nodo intermedio K. Tutte le d.d.p. sulla maglia AKD possono essere scritte considerando convenzionalmente positivo il verso orario per le tensioni:
![]() ,
,
per cui confermiamo l’equazione:
![]()
Per il calcolo della ![]() osserviamo la maglia ABD e scriviamo la legge di Kirchhoff:
osserviamo la maglia ABD e scriviamo la legge di Kirchhoff:
![]()
otteniamo:
![]()
La corrente ![]() è facilmente ottenibile applicando la Ia legge di Kirchhoff al nodo B:
è facilmente ottenibile applicando la Ia legge di Kirchhoff al nodo B:
![]()
Calcolo della resistenza 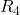
Se conoscessimo ![]() , potremmo ottenere
, potremmo ottenere ![]() dall’equazione:
dall’equazione:
![]()
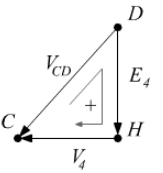
Infatti, osservando la situazione fra i nodi C e D e quello intermedio H, avremo con verso positivo per le tensioni:
![]() che porta a:
che porta a:
![]()
Conoscendo ![]() e
e ![]() , l’equazione diventa:
, l’equazione diventa:
![]()
Troveremo ![]() con l’equazione precedente:
con l’equazione precedente:
![]()