Blog di Megistone

Megistone - Per non perdere l'orientamento

Esercizio 8: Soluzione

 

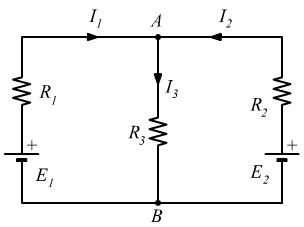
Dati noti

  • E_1 = 11\,\text{V}
  • E_2 = 7\,\text{V}
  • E_3 = 2\,\text{V}
  • R_1 = 1\,\Omega, \quad R_2 = 1\,\Omega, \quad R_3 = 1\,\Omega
  • I_3 = 2\,\text{A}

Legge di Kirchhoff al nodo A

I_3 = I_1 + I_2

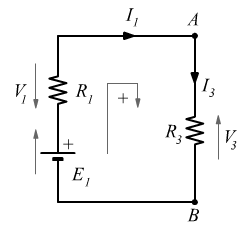
Equazione della maglia sinistra

0 = E_1 - V_{R_1} - V_{R_3} \Rightarrow E_1 = R_1 I_1 + R_3 I_3

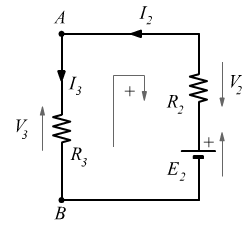
Equazione della maglia destra

0 = V_{R_3} + V_{R_2} - E_2 \Rightarrow E_2 = R_2 I_2 + R_3 I_3

 

\left\{ \begin{array}{l} I_3 = I_1 + I_2 \\ E_1 = R_1 I_1 + R_3 I_3 \\ E_2 = R_3 I_3 + R_2 I_2 \\ \end{array} \right. \quad \left\{ \begin{array}{l} I_3 - I_2 = I_1 \\ E_1 = R_1 I_1 + R_3 I_3 \\ E_2 = R_3 I_3 + R_2 I_2 \\ \end{array} \right.

\left\{ \begin{array}{l} E_1 = R_1 (I_3 - I_2) + R_3 I_3 \\ E_2 = R_3 I_3 + R_2 I_2 \\ \end{array} \right. \quad \left\{ \begin{array}{l} E_1 = (R_1 + R_3) I_3 - R_1 I_2 \\ E_2 = R_3 I_3 + R_2 I_2 \\ \end{array} \right.

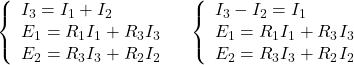
Inserendo i valori

\begin{array}{ll} 11 = (2 + 1)I_3 - 2I_2 & \quad \text{(ossia } 11 = 3I_3 - 2I_2\text{)} \\ 7 = I_3 + I_2 & \quad \Rightarrow \quad 7 - I_2 = I_3 \\ \end{array}

Sostituendo 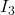\( I_3 \) nell’espressione sopra:

    \begin{align*} \hspace{-5cm} 11 &= 3(7 - I_2) - 2I_2 \\ 11 &= 21 - 3I_2 - 2I_2 \\ 11 &= 21 - 5I_2 \\ 5I_2 &= 21 - 11 \\ 5I_2 &= 10 \\ I_2 &= \frac{10}{5} = 2\,\text{A} \end{align*} }

 

 

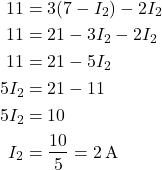
Sostituendo tale valore nella 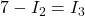\( 7 - I_2 = I_3 \):

I_3 = 7 - 2 = 5\,\text{A}

Ricaviamo infine:

I_1 = I_3 - I_2 = 5 - 2 = 3\,\text{A}

Articoli correlati

Esercizio 12: Soluzione

Esercizio 11: Soluzione

Esercizio 10: Soluzione

Let’s Create Your Own Event Group.

Blog di Megistone

Megistone - Per non perdere l'orientamento

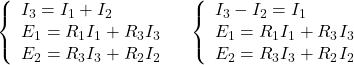
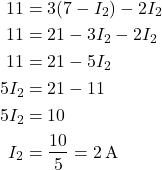
Proudly powered by WordPress | Tema: Newsup di Themeansar.