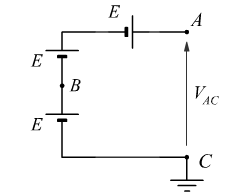
Cinque generatori uguali di valore ![]() vengono collegati secondo il seguente schema. Calcola il valore dei potenziali dei punti A, C e B:
vengono collegati secondo il seguente schema. Calcola il valore dei potenziali dei punti A, C e B:
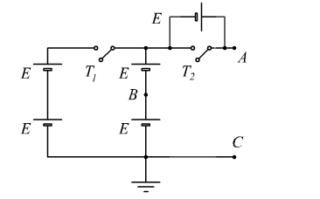
- con
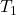 e
e 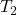 chiusi
chiusi - con
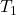 e
e 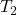 aperti
aperti
Soluzione – Caso 1)
L’ultimo generatore in alto a destra è cortocircuitato, quindi si può ignorare.
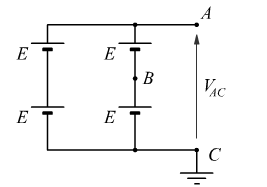
Abbiamo due rami in parallelo tra i punti A e C, ciascuno composto da due generatori in serie:
![]()
Poiché i generatori sono uguali e perfettamente simmetrici, il punto B si trova esattamente a metà tra A e C, quindi:
![]()
Soluzione – Caso 2)
Il deviatore ![]() è aperto e quindi esclude il ramo di sinistra. Il circuito diventa:
è aperto e quindi esclude il ramo di sinistra. Il circuito diventa:
I tre generatori restanti sono in serie e concordi: la tensione tra A e C è quindi:
![]()
Poiché il nodo ![]() è a massa (
è a massa (![]() ), si ha:
), si ha:
![]()
Il punto ![]() si trova esattamente dopo il primo generatore rispetto al nodo di massa, quindi subisce un incremento di:
si trova esattamente dopo il primo generatore rispetto al nodo di massa, quindi subisce un incremento di:
![]()