Esercizio n.10 – Calcolo della resistenza equivalente
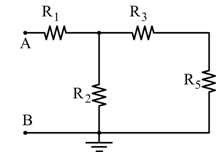
Analizziamo il circuito in quattro diverse configurazioni, a seconda dello stato degli interruttori T₁ e T₂. In ogni caso, calcoliamo la resistenza equivalente tra i punti A e B.
Dati del problema
\(\begin{aligned}
R_1 &= 2{,}7\,\text{k}\Omega \\
R_2 &= 8\,\text{k}\Omega \\
R_3 &= 0{,}4\,\text{k}\Omega \\
R_4 &= 1\,\text{k}\Omega \\
R_5 &= 6\,\text{k}\Omega
\end{aligned}
\)
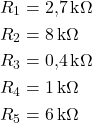
✅ Caso A: T₁ aperto, T₂ chiuso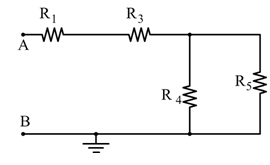
\(R_{AB} = R_1 + R_3 + \frac{R_4 \cdot R_5}{R_4 + R_5}
\) \(
R_{AB} = 2{,}7 + 0{,}4 + \frac{1 \cdot 6}{1 + 6} = \boxed{3{,}95\,\text{k}\Omega}
\)
✅ Caso B: T₁ chiuso, T₂ aperto
R_{AB} = R_1 + \frac{R_2 \cdot (R_3 + R_5)}{R_2 + R_3 + R_5}
\) \(
R_{AB} = 2{,}7 + \frac{8 \cdot 1{,}4}{9{,}4} = \boxed{3{,}89\,\text{k}\Omega}
\)
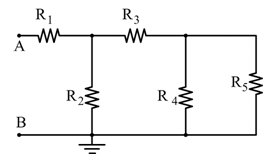
✅ Caso C: T₁ e T₂ chiusi
R_{AB} = R_1 + \frac{R_2 \cdot \left( R_3 + \frac{R_4 \cdot R_5}{R_4 + R_5} \right)}{R_2 + R_3 + \frac{R_4 \cdot R_5}{R_4 + R_5}}
\) \(
R_{AB} = 2{,}7 + \frac{8 \cdot 1{,}25}{9{,}25} = \boxed{3{,}78\,\text{k}\Omega}
\)
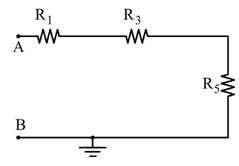
✅ Caso D: T₁ e T₂ aperti
R_{AB} = R_1 + R_3 + R_5 = 2{,}7 + 0{,}4 + 1 = \boxed{4{,}1\,\text{k}\Omega}
\)
📊 Confronto finale
\(\begin{array}{|c|c|c|}
\hline
\textbf{Configurazione} & \textbf{Interruttori} & \boldsymbol{R_{AB}\,(\text{k}\Omega)} \\
\hline
\text{Caso A} & T_1 \text{ aperto}, T_2 \text{ chiuso} & 3{,}95 \\
\text{Caso B} & T_1 \text{ chiuso}, T_2 \text{ aperto} & 3{,}89 \\
\text{Caso C} & T_1 \text{ chiuso}, T_2 \text{ chiuso} & 3{,}78 \\
\text{Caso D} & T_1 \text{ aperto}, T_2 \text{ aperto} & 4{,}10 \\
\hline
\end{array}
\)