Dom. Giu 15th, 2025

Esercizio n.13

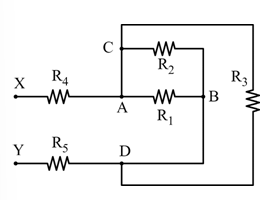
Esercizio n.13 – Soluzione con cortocircuiti e resistenze in parallelo

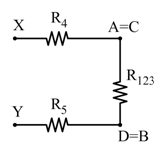
Notiamo che, a causa dei cortocircuiti, alcuni nodi coincidono: A = C e B = D. Ne consegue che R₁ e R₂ sono in parallelo:

$R_{12} = R_1 // R_2 = \frac{2 \cdot 1}{2 + 1} = \frac{2}{3} = 0{,}67\,\text{k}\Omega$

Secondo passaggio: parallelo tra R₁₂ e R₃

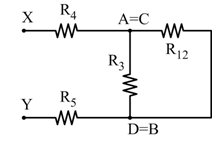
$R_{123} = R_3 // R_{12} = \frac{3 \cdot \frac{2}{3}}{3 + \frac{2}{3}} = \frac{2}{\frac{11}{3}} = \frac{6}{11}\,\text{k}\Omega$

Resistenza totale tra X e Y

Essendo R₁₂₃ in serie con R₄ e R₅ , la resistenza totale si calcola così:

$R_{XY} = R_4 + R_{123} + R_5 = 0{,}4 + \frac{6}{11} + 0{,}5 = \boxed{1{,}445\,\text{k}\Omega}$

Articoli correlati

Esercizio n.12

Esercizio n.11

Esercizio n.10