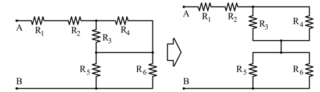
Caso A)
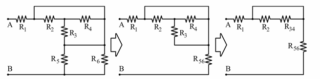
Si riconosce che:
![]()
![Rendered by QuickLaTeX.com \[ R_{AB} = (50 + 50) + \frac{300 \cdot 300}{300 + 300} = 100 + 150 = 250\,\Omega \] [latex] \bigskip \textbf{Caso B)} [latex] \[ R_{AB} = R_1 + \left\{ R_6 \parallel \left[ (R_2 \parallel R_4) + R_3 + R_5 \right] \right\} \]](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-b1c79553bf2ed6f16d458716df5ad6b8_l3.png)
![]()
\bigskip
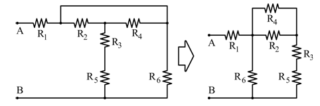
\textbf{Caso C)}
![]()
![]()
\bigskip
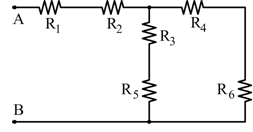
\textbf{Caso D – Deviatori entrambi chiusi:}
![]()
Megistone - Per non perdere l'orientamento



Caso A)

Si riconosce che:
![]()
![Rendered by QuickLaTeX.com \[ R_{AB} = (50 + 50) + \frac{300 \cdot 300}{300 + 300} = 100 + 150 = 250\,\Omega \] [latex] \bigskip \textbf{Caso B)} [latex] \[ R_{AB} = R_1 + \left\{ R_6 \parallel \left[ (R_2 \parallel R_4) + R_3 + R_5 \right] \right\} \]](https://www.megistone.it/wp-content/ql-cache/quicklatex.com-b1c79553bf2ed6f16d458716df5ad6b8_l3.png)
![]()
\bigskip
\textbf{Caso C)}
![]()
![]()
\bigskip
\textbf{Caso D – Deviatori entrambi chiusi:}
![]()