Potenze nei sistemi trifase -

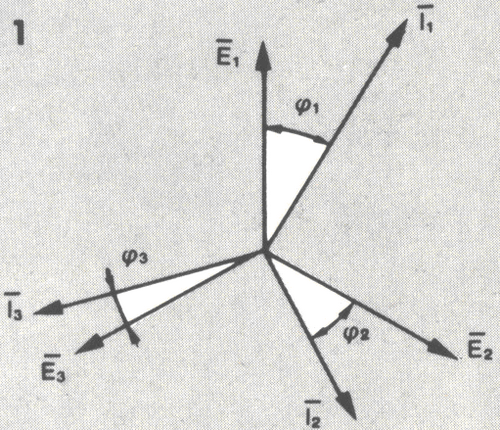
La potenza elettrica di un sistema trifase si basa sulle considerazioni fatte a proposito del caso monofase, poiché questo, come detto in precedenza, è equivalente a tre sistemi monofasi facenti capo a un centro O (centro stella). Quindi la potenza elettrica istantanea di un sistema trifase può essere sempre espressa dalla somma dei prodotti dei valori istantanei della tensione e della corrente di ciascuna fase. Possiamo scrivere:

$p(t) = e_1(t)i_1(t) + e_2(t)i_2(t) + e_3(t)i_3(t)$

dove $e_1, i_1, e_2, i_2, e_3, i_3$ indicano la tensione e la corrente (rispettivamente della prima, seconda e terza fase) che caratterizzano il circuito trifase nella sezione considerata.
Come nei sistemi monofasi, interessa conoscere la potenza reale, definita come il valor medio della potenza istantanea. Essa può essere espressa come somma delle potenze reali delle singole fasi:

$P = V_1 I_1 \cos\varphi_1 + V_2 I_2 \cos\varphi_2 + V_3 I_3 \cos\varphi_3$

dove $\varphi_1$ è l’angolo di sfasamento fra $V_1\) e \(I_1$ (valori efficaci), e così per $\varphi_2, \varphi_3$ .

diagramma vettoriale tensioni e correnti — Figura 1 – Diagramma vettoriale delle tensioni e correnti di fase.

La potenza reattiva $Q$ è definita come somma algebrica delle potenze reattive delle singole fasi:

$Q = V_1 I_1 \sin\varphi_1 + V_2 I_2 \sin\varphi_2 + V_3 I_3 \sin\varphi_3$

La potenza apparente si ricava dalla formula generale:

$S = \sqrt{P^2 + Q^2}$

È errato scrivere $S = V_1 I_1 + V_2 I_2 + V_3 I_3$ , perché i singoli prodotti rappresentano potenze apparenti parziali con direzioni diverse: tale espressione vale solo in sistemi equilibrati e simmetrici.
Il fattore di potenza complessivo è:

$\cos\varphi = \frac{P}{S} = \frac{P}{\sqrt{P^2 + Q^2}}$

Se il sistema è simmetrico nelle tensioni ( $E_1=E_2=E_3$ ) ed equilibrato nelle correnti ( $I_1=I_2=I_3$ ), gli angoli di sfasamento sono uguali:

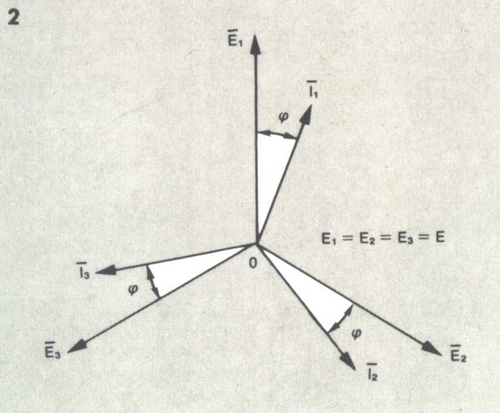
diagramma vettoriale simmetrico — Figura 2 – Sistema trifase simmetrico ed equilibrato.

$\varphi_1 = \varphi_2 = \varphi_3 = \varphi$

In tal caso la potenza attiva e reattiva assumono forme compatte:

$P = 3 V_f I_f \cos\varphi = \sqrt{3} V_{LL} I_L \cos\varphi$
$Q = 3 V_f I_f \sin\varphi = \sqrt{3} V_{LL} I_L \sin\varphi$
$S = 3 V_f I_f = \sqrt{3} V_{LL} I_L$

Table of Contents

Esempio numerico

Un utilizzatore trifase è alimentato con $V_{LL}=380\ \text{V}$ , ha impedenza per fase $|Z|=20\ \Omega$ e fattore di potenza 0,8. Calcoliamo P, Q, S per stella e triangolo.

Collegamento a stella:

$V_f = \frac{380}{\sqrt{3}} \approx 219,4\ \text{V}\ \ I_f=I_L=\frac{219,4}{20}\approx 10,97\ \text{A}$

$P = \sqrt{3} V_{LL} I_L \cos\varphi = \sqrt{3}\cdot 380 \cdot 10,97 \cdot 0,8 \approx 5,78\ \text{kW}$
$Q = \sqrt{3} V_{LL} I_L \sin\varphi = \sqrt{3}\cdot 380 \cdot 10,97 \cdot 0,6\approx 4,33\ \text{kVAr}$
$S = \sqrt{P^2+Q^2} = \sqrt{3}\cdot 380 \cdot 11 \approx 7,22\ \text{kVA}$

Collegamento a triangolo:

$V_f = V_{LL} = 380\ \text{V}\ \ I_f = \frac{380}{20}=19\ \text{A}\ \ I_L=\sqrt{3} I_f \approx 32,9\ \text{A}$

$P = \sqrt{3} V_{LL} I_L \cos\varphi = \sqrt{3}\cdot 380 \cdot 32,87 \cdot 0,8 \approx 17,33\ \text{kW}$

$Q = \sqrt{3} V_{LL} I_L \sin\varphi = \sqrt{3}\cdot 380 \cdot 32,87 \cdot 0,6 \approx 13\ \text{kVAr}$

$S = \sqrt{P^2+Q^2} = \sqrt{3}\cdot 380 \cdot 32,9 \approx 21,66\ \text{kVA}$

Confrontando i due casi, in triangolo la corrente e le potenze sono circa tre volte maggiori rispetto alla stella, a parità di tensione concatenata e impedenza di fase.

Metodo di Boucherot

È opportuno comunque richiamare l’utilità del metodo di Boucherot nella risoluzione dei problemi connessi a circuiti trifasi. Questo metodo è particolarmente utile quando si devono studiare sistemi che mettono in gioco più elementi energetici.
Una linea trifase a 380 V alimenta un forno trifase da $P_1=15\ \text{kW}$ (cosφ=1) e un motore trifase da $P_2=20\ \text{kW}$ con cosφ=0,75. Calcoliamo la corrente di linea e il fattore di potenza totale.

$Q_1=0\ \ Q_2 = P_2 \tan\varphi = 20\cdot 0,88 \approx 17,6\ \text{kVAr}$

$P = P_1+P_2=35\ \text{kW}\ \ Q=17,6\ \text{kVAr}$

$S=\sqrt{P^2+Q^2}\approx 39,2\ \text{kVA}\ \ cos\varphi=\frac{P}{S}\approx 0,893$

$I_L = \frac{S}{\sqrt{3}\,V_{LL}} = \frac{39,2\ \text{kVA}}{\sqrt{3}\cdot 380\ \text{V}} \approx 59,5\ \text{A}$

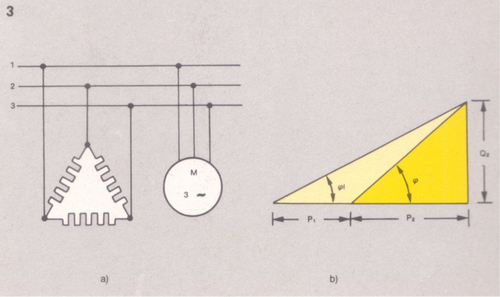
triangolo delle potenze — Figura 3 – Triangolo delle potenze (metodo di Boucherot).

Tabella riassuntiva – Potenze nei sistemi trifase

Collegamento	Relazioni tensione/corrente	Potenza attiva (P)	Potenza reattiva (Q)	Potenza apparente (S)
Stella	$V_{LL} = \sqrt{3}\, V_f$ $I_L = I_f$	$P = \sqrt{3}\, V_{LL} I_L \cos\varphi$	$Q = \sqrt{3}\, V_{LL} I_L \sin\varphi$	$S = \sqrt{3}\, V_{LL} I_L$
Triangolo	$V_f = V_{LL}$ $I_L = \sqrt{3}\, I_f$	$P = \sqrt{3}\, V_{LL} I_L \cos\varphi$	$Q = \sqrt{3}\, V_{LL} I_L \sin\varphi$	$S = \sqrt{3}\, V_{LL} I_L$